从零构建数字滤波器
滤波器在信号处理、控制系统等领域起着十分重要的作用。然而,在实际的数字信号处理中,过于简单的 IIR(Infinite Impulse Response)滤波器结构会引入数值精度的影响,甚至可能导致滤波器发散。为了便于构造稳定的滤波器,本文将具体梳理 数字滤波器的实现步骤,并给出简单的推导和必要的伪代码步骤。
基本思路
从线性系统理论层面讲,拉普拉斯变换可以更方便地分析系统的频率响应,因此我们首先会在 $s$ 域完成模拟滤波器(Analog Filter)的设计。特别地,得益于 $s$ 域的变换,我们可以根据滤波器原型变换得到各种形式的滤波器。然后进行一定的离散化变换即可得到数字滤波器(Digital Filter)。
从稳定性上来看,滤波器是否稳定取决于极点分布,因此模拟滤波器可用零极点(Zero-Pole-Gain,通常简称 zpk)的形式表示,以减少数值误差的影响。而在数值计算上看,数字滤波器的阶数不易太高,以避免状态量之间存在量级差异而引入计算误差,所以实际会将高阶滤波器拆解为串联的二阶节(SOS:Second-Order Sections)形式。
简言之,数字滤波器的实现可以分为以下几个步骤:
- 设计模拟滤波器的原型,得到 $s$ 域的零极点分布;
- 根据频域变换,将滤波器原型变换为符合需求的模拟滤波器;
- 根据采样率对滤波器参数离散化,得到 $z$ 域的零极点分布;
- 将 $z$ 域的零极点匹配,拆解为多个二阶节并排序;
- 按照二阶系统的处理方法依次处理二阶节即可实现滤波。
需要注意的是,离散化通常采用 双线性变换,因此在上述第二步进行 $s$ 域的变换前需要对频率进行 预畸。
常用滤波器原型
我们在 信号的滤波 讨论过滤波器的基本参数和四种常见的滤波器,此处不再赘述。模拟滤波器的零极点形式为:
$$ H(s) = g \frac{(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)} = g \frac{\prod_{k=1}^m (s - z_k)}{\prod_{k=1}^n (s - p_k)} ,\quad g > 0 $$其中 $z_k \; (k = 1,2,\dots,m)$ 为零点,$p_k \; (k = 1,2,\dots,n)$ 为极点。稳定的、非最小相位系统零极点的实部均小于零;进一步,适定系统的分子的阶次不超过分母,即 $m \le n$。特别地,如果系统不存在有限的零点(零点在无穷远),此时传递函数的分子为常数。
滤波器原型通常是指转折频率为 $1\,\mathrm{rad/s}$ 的低通滤波器,下面我们将归纳几种常见滤波器原型的零极点分布。
巴特沃斯滤波器
巴特沃斯滤波器(Butterworth Filter)是通带最平坦的滤波器。能量衰减一半(幅值衰减 $\sqrt{2}/2$)对应的频率为转折频率,也是我们常说的 $-3 \,\mathrm{dB}$ 带宽。
巴特沃斯滤波器原型不存在有限零点,$N$ 阶滤波器原型的极点均匀分布在复平面单位圆左侧,即:
$$ \bar{p}_k = \mathrm{e}^{-j\theta_k}, \quad \theta_k = \frac{2k + N - 1}{2N} \pi , \quad k = 1,2,\dots, N $$巴特沃斯滤波器原型直流增益为 $1$,无须再进行修正,因而 $\bar{g} = 1$。
为了与一般滤波器的零极点进行区分,本文将使用上横线表示滤波器原型的零极点。进一步,记滤波器原型的零极点数量分别为 $\bar{m} \le \bar{n}$,
切比雪夫 I 型滤波器
切比雪夫 I 型滤波器(Type I Chebyshev Filter)允许在转折频率表示的带宽以内,滤波器的增益在 $[1/\sqrt{1 + \varepsilon^2}, \, 1]$ 之间波动。
切比雪夫 I 型滤波器同样没有零点,指定通带纹波系数 $\varepsilon > 0$,$ N $ 阶滤波器原型的极点按照辐角均匀分布在复平面椭圆左侧,可以根据下式计算:
$$ \bar{p}_k = \sinh \mu \cos \theta_k + j \cosh \mu \sin \theta_k , \quad \mu = \frac{1}{N} \mathrm{arsinh} \frac{1}{\varepsilon} , \quad \theta_k = \frac{2k + N - 1}{2N} \pi , \quad k = 1,2,\dots, N $$为了将直流增益修正到 $1$,需要补充增益:
$$ \bar{g} = \frac{1}{2^{N-1} \varepsilon} $$切比雪夫 II 型滤波器
切比雪夫 II 型滤波器(Type II Chebyshev Filter)具有平坦的通带和波动的阻带,阻带增益不高于 $\varepsilon / \sqrt{1 + \varepsilon^2}$,转折频率定义为幅频响应第一次低于阻带增益的频率。
$N$ 阶切比雪夫 II 型滤波器的极点与 I 型滤波器的极点互为倒数,为:
$$ \bar{p}_k = \frac{1}{\sinh \mu \cos \theta_k + j \cosh \mu \sin \theta_k} , \quad \mu = \frac{1}{N} \mathrm{arsinh} \frac{1}{\varepsilon} , \quad \theta_k = \frac{2k + N - 1}{2N} \pi , \quad k = 1,2,\dots, N $$此外,切比雪夫 II 型滤波器还有 $N$ 个零点:
$$ \bar{z}_k = \frac{j}{\sin\theta_k}, \quad \theta_k = \frac{2k + N - 1}{2N} \pi, \quad k = 1,2,\dots, N $$特别注意的是,当 $N$ 为奇数时,存在一个无穷远处的零点(分母为 0),在显式的零极点表述中可以忽略。
直流增益的补偿需要引入增益:
$$ \bar{g} = \prod_{k=1}^N \frac{\bar{p}_k}{\bar{z}_k} $$同样注意,实数系数滤波器的零极点都是以实数或共轭复数对的形式存在,因此上述增益一定是实数。在程序设计中由于数值误差的存在,需要额外取结果的实部。
滤波器原型变换
在拉普拉斯变换下,通过对 $s$ 进行一定的替换,可以将模拟滤波器原型转化为各种其他形式,下面我们将讨论对应零极点的变换。
注意,为了与后面双线性变换的离散化方法对应,滤波器原型变换前需要对目标频率进行预畸。假设最终的数字滤波器的转折频率为 $f_d < f_s / 2$(对应的角频率为 $\omega_d = 2 \pi f_d$),其中 $f_s$ 为采样率。那么在设计模拟滤波器时,转折频率应当取:
$$ f_c = \frac{f_s}{\pi} \tan \left( \frac{f_d}{f_s} \pi \right) $$低通变换
为了将低通滤波器原型转化为任意截止频率 $\omega_c$ 的低通滤波器,只需要将 $s$ 替换为 $s/\omega_c$ 即可。以极点变换为例:
$$ \prod_{k=1}^N (s - \bar{p}_{k}) \; \rightarrow \; \prod_{k=1}^N \left(\frac{s}{\omega_c} - \bar{p}_k \right) $$因此对应的极点只需要进行线性变换:
$$ p_k = \bar{p}_k \omega_c $$零点的变换与极点相同,但需要注意滤波器原型的零极点数量不一定相等,对应的索引 $k$ 的范围不一定相同。此时还应当根据相对阶数对增益进行调整,为:
$$ g = \bar{g} \omega_c^{\bar{n} - \bar{m}} $$高通变换
类似地,为了得到转折频率为 $\omega_c$ 的高通滤波器,需要将 $s$ 替换为 $\omega_c/s$。同样以极点为例:
$$ \prod_{k=1}^N (s - \bar{p}_{k}) \; \rightarrow \; \prod_{k=1}^N \left(\frac{\omega_c}{s} - \bar{p}_k \right) $$因此极点变换与滤波器原型极点的倒数相关,为:
$$ p_k = \frac{\omega_c}{\bar{p}_k} $$零点的变换相同。需要特别注意的是,我们在记录零点时并没有显式地记录无穷处的零点,而上述倒数变换会将无穷远出的零点映射到原点处的零点(成为有限值),因此还需要根据滤波器原型的相对阶数补充 $\gamma$ 个 $z = 0$ 的零点。
考虑无穷大频率处的增益归一,上述变换后取 $s \to \infty$,可见需要将增益修正为:
$$ g = \bar{g} \frac{\prod_{k=1}^{\bar{m}}\bar{z}_k}{\prod_{k=1}^{\bar{n}}\bar{p}_k} $$带通变换
带通变换通常是将 $s$ 替换为 $(s^2 + \omega_0^2) / (\xi s)$ 来实现,注意到滤波器的阶次将会翻倍。考虑到:
$$ s - \bar{p}_k = 0 \; \rightarrow \; \frac{s^2 + \omega_0^2}{\xi s} - \bar{p}_k = 0 $$可知滤波器原型的每个极点将分裂为两个,分别为:
$$ p_{k, k'} = \frac{1}{2} \left( \bar{p}_k \xi \pm \sqrt{(\bar{p}_k \xi)^2 - 4 \omega_0^2} \right) $$零点的变换相似,但当极点阶数比零点高时,每个无穷远处的零点会分裂成一个原点处的零点和无穷远的零点。因此还要根据相对阶数追加 $n - m$ 个原点处的零点。
最后根据滤波器原型的相对阶数对增益修正为:
$$ g = \bar{g} \xi^{\bar{n}-\bar{m}} $$上述变换中的中心频率 $\omega_0$ 和带宽系数 $\xi$ 不够直观,实际应用一般使用通带频率 $\omega_1 < \omega_2$ 来表示,考虑在通带边缘对应滤波器原型的截止频率,在变换前后分别代入 $s = j$ 和 $s = j\omega_{1,2}$,有:
$$ \left\lvert\frac{(j\omega_{1,2})^2 + \omega_0^2}{j \xi \omega_{1,2}}\right\rvert = \lvert j \rvert $$考虑 $\omega_1 < \omega_0 < \omega_2$,则有:
$$ \left\{ \begin{aligned} \omega_0^2 - \omega_1^2 = \xi \omega_1 \\ \omega_2^2 - \omega_0^2 = \xi \omega_2 \\ \end{aligned} \right. $$解得:
$$ \omega_0 = \sqrt{\omega_1 \omega_2} ,\quad \xi = \omega_2 - \omega_1 $$带阻变换
与带通变换相反,将 $s$ 替换为 $\xi s / (s^2 + \omega_0^2)$ 即可。类似地,有:
$$ s - \bar{p}_k = 0 \; \rightarrow \; \frac{\xi s}{s^2 + \omega_0^2} - \bar{p}_k = 0 $$极点的变换为:
$$ p_k = \frac{1}{2\bar{p}_k} \left( \xi \pm \sqrt{\xi^2 - 4 \bar{p}_k^2 \omega_0^2} \right) $$零点变换相似。特别地,如果滤波器原型的相对阶次 $\bar{n} > \bar{m}$,即原型存在无穷远处的零点,应当相应地补充 $\bar{n} - \bar{m}$ 个 $\pm j\omega_0$ 的零点对。
增益修正为:
$$ g = \bar{g} \frac{\prod_{k=1}^{\bar{m}}\bar{z}_k}{\prod_{k=1}^{\bar{n}}\bar{p}_k} $$与带通滤波器相似,如果用带阻滤波器的阻带频率 $\omega_{1,2}$ 表示,中心频率和带宽系数与阻带起止频率的关系为:
$$ \omega_0 = \sqrt{\omega_1 \omega_2} ,\quad \xi = \omega_2 - \omega_1 $$滤波器离散化
数字滤波器离散化通常采用双线性变换的方法,其基本原理可以看作是连续时间的积分按照相邻两个时刻数据的梯形面积近似。为了避免画图示意,这里给出数学来源,考虑 $z$ 变换与拉普拉斯变换之间的关系:
$$ z = \mathrm{e}^{T_ss} = \frac{\mathrm{e}^{ \frac{T_s}{2}s}}{\mathrm{e}^{ -\frac{Ts}{2}s}} \approx \frac{1 + \frac{T_s}{2} s}{1 - \frac{T_s}{2} s} = \frac{2f_s + s}{2f_s -s} $$其中 $T_s = 1/ f_s$ 为采样时间。将上式最后的 $s$ 替换为模拟器滤波器的零极点,就分别得到了离散化的零极点。
需要注意的是,当模拟滤波器传递函数分母的阶次比分子高时,意味着有 $n-m$ 个零点分布在无穷远处,根据上式变换后将会被映射为 $-1$。由于无穷远处的零点没有显式地记录下来,因此离散化变换后需要手动补充 $n-m$ 个位于 $-1$ 处的零点,此时数字系统的零极点数量相同。
离散化变换后应当注意对增益进行修正:
$$ g \rightarrow g \frac{\prod_{k=1}^{m}(2f_s - z_k)}{\prod_{k=1}^{n}(2 f_s + p_k)} $$箭头右侧的参数均为模拟滤波器的零极点和增益。
下面我们补充一点双线性变换的频率映射,反解上面的双线性变换对应,得到对应的 $s$ 显式替换策略:
$$ s \rightarrow \frac{2}{T_s} \frac{z-1}{z+1} $$记 $\omega_c$ 为模拟滤波器的频率,$\omega_d$ 为离散化后数字滤波器的频率,根据双线性变换的规则可知:
$$ j\omega_c \rightarrow \frac{2}{T_s} \frac{\mathrm{e}^{jT_s \omega_d} -1}{\mathrm{e}^{jT_s \omega_d}+1} = \frac{2}{T_s} \frac{\mathrm{e}^{jT_s \omega_d/2} -\mathrm{e}^{-jT_s \omega_d/2}}{\mathrm{e}^{jT_s \omega_d/2}+\mathrm{e}^{-jT_s \omega_d/2}} = j \frac{2}{T_s} \tan \frac{T_s \omega_d}{2} $$化简即可得到自然频率之间的关系为:
$$ f_c = \frac{f_s}{\pi} \tan \left( \frac{f_d}{f_s} \pi \right) $$这就是我们前面提到的预畸公式。为了正确预畸,数字滤波器的截止频率必须小于奈奎斯特频率,即 $f_c < f_s / 2$。相反,双线性变换可以将模拟滤波器的全频段通过反正切函数映射到 $[0, f_s/2)$ 范围内,可以避免由于频率映射导致的 “离散化混叠”。
数字滤波器集成
至此,我们得到了数字滤波器的零极点,且零极点的数量相同,以实数或共轭复数对的形式存在。为了减少数值计算误差,我们将把高阶滤波器拆解为多个二阶数字滤波器,每个数字滤波器的传递函数为:
$$ H(s) = \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}} $$注意我们以 $z^{-1}$ 为变量,一方面便于数字滤波器的实现;另一方面指出通过令 $b_2 = a_2 = 0$ 也能兼容一阶系统。当数字滤波器的阶次为奇数时将会产生一个一阶环节。
将拆解出来的多个二阶滤波器系数组合为矩阵,即构成所谓的 SOS 矩阵:
$$ \mathrm{SOS} = \begin{bmatrix} b_{00} & b_{01} & b_{02} & 1 & a_{01} & a_{02} \\ b_{10} & b_{11} & b_{12} & 1 & a_{11} & a_{12} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ b_{n0} & b_{n1} & b_{n2} & 1 & a_{n1} & a_{n2} \\ \end{bmatrix} $$二阶节转换
将数字滤波器的零极点转化二阶节需要把握以下基本原则:
- 复数极点必须成对匹配后构成一个二阶系统,以确保滤波器系数为实数;零点同理;
- 如果存在多个实数极点,应当匹配两个实数极点,零点同理;
- 如果只有一个实数极点,一定与实数零点进行匹配;
- 二阶系统的零极点尽可能接近,以避免出现较大的增益变化。
此外,二阶系统的排序稍有讲究,一般对应大带宽的快速极点构成的二阶系统靠前,小带宽的慢速极点(靠近单位圆,最不利极点)的慢速极点靠后。实际滤波时表现为“滤波带宽逐渐减小”的形式。通常会先从最慢的极点查找,零极点匹配构成二阶系统后之后再反向排序。
二阶节转换的算法可以用伪代码表示如下:
初始化 sos 矩阵为空
如果剩余极点数量不为零,重复执行以下操作:
# 首先查找极点
从极点列表中弹出一个最不利极点,记为 p1
如果 p1 是实数:
如果剩余的极点列表中还有实数极点:
从极点列表中弹出一个最接近 p1 的实数极点,记为 p2
否则(没有其他实数极点,意味着这次零极点匹配为一阶系统):
从零点列表中弹出一个最接近 p1 的实数零点,记为 z1
根据 p1、z1 计算一阶系统的传递函数系数,并追加到 sos 矩阵中
执行下一次循环
否则(p1 为复数):
取 p2 为 p1 的共轭,并从极点列表中删除 p2
# 然后匹配零点:由于一阶系统提前退出循环,这里一定是找两个零点
从零点列表中找到最接近 p1 的零点,记为 z1,先不要删除
如果 z1 是实数:
如果零点列表中除了 z1 还有其他实数零点:
从零点列表中删除 z1
从零点列表中弹出最接近 p1 的另一个实数零点,记为 z2
如果零点列表中没有其他实数零点(那么这个 z1 必须保留给最后的一阶环节):
从零点列表中弹出最接近 p1 的复数零点,记为 z1
取 z2 为 z1 的共轭,并从零点列表中删除 z2
根据 p1、p2、z1、z2 计算二阶系统传递函数系数,并追加到 sos 矩阵中
将 sos 矩阵按行逆序即可数据滤波
基于 SOS 矩阵对输入进行滤波时,只需要按照二阶系统依次滤波即可。每个二阶系统可以按照 Direct Form II 的形式进行滤波。
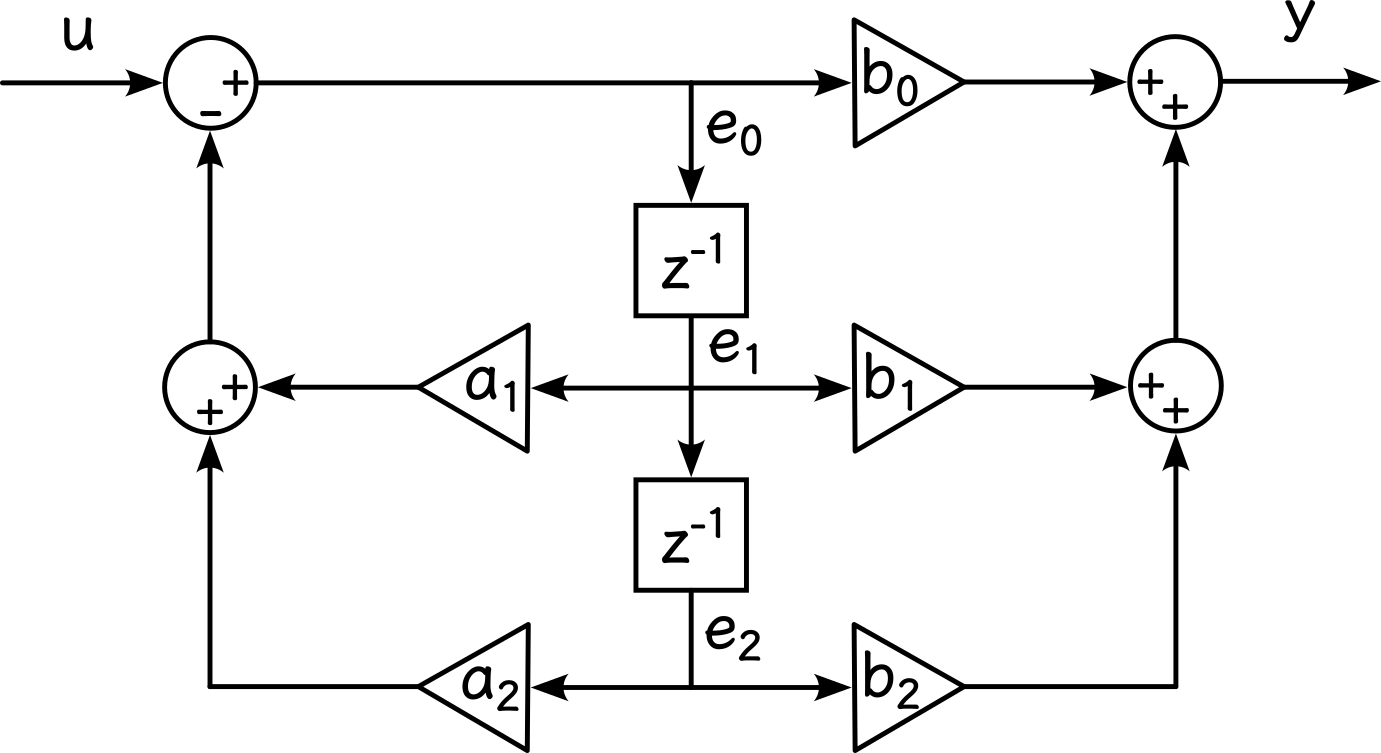
二阶系统的滤波以 Python 代码为例:
e2 = e1
e1 = e0
e0 = u - a1 * e1 - a2 * e2
y = b0 * e0 + b1 * e1 + b2 * e2稳态重置
为了避免滤波器初始状态引入的收敛过程,我们会希望将滤波器的状态按照给定的数据重置内部状态,表现为 “一直输入固定值直到滤波器达到稳态” 的效果。从上述 Direct From II 的结构可以看到,滤波器内部的状态只与传递函数的分母多项式相关。当达到稳态时,有:
$$ e_0 = e_1 = e_2 = \frac{u}{1 + a_1 + a_2} $$