文章 分类 标签 关于

目录

目录

周期系统稳定性与 Floquet 理论简介

大春雨 avatar  收录于  类别 控制理论基础
     约 1853 字   预计阅读 9 分钟 

周期系统是指系统参数随着时间以某一固定周期变化的动态系统，Floquet 理论为我们提供了一种有效的方法来研究这类系统的稳定性。本文将简要介绍 Floquet 理论的基本概念，并给出一个简单的示例来说明其应用。

说明
本文的正文会从数学上对线性时变微分方程的通解进行讨论，为了帮助读者快速了解其与周期系统稳定性之间的关系，简要梳理其思路为：周期系统的通解与一个常数矩阵 $B$ 呈现周期性关系，该矩阵的特征值对因通解的包络，其模长决定了系统的稳定性。

考虑如下的线性时变微分方程：

$$ \dot{\bm{x}}(t) = A(t) \bm{x}(t) $$

其中 $A(t)$ 以 $T$ 为周期。假设 $\bm{x}_1(t), \, \bm{x}_2(t) , \dots , \bm{x}_n(t)$ 为上述方程的一组线性独立的解，将其按列向量拼接为矩阵 $X(t)$，称之为基础矩阵（Fundamental Matrix） ，即：

$$ X(t) = \begin{bmatrix} \bm{x}_1(t) & \bm{x}_2(t) & \dots & \bm{x}_n(t) \end{bmatrix} $$

同时，记 $W(t) = \left\lvert X(t) \right\rvert$ 为基础矩阵的行列式（Wronskian 行列式），容易证明：

$$ W(t) = W(t_0) \exp\left( \int_{t_0}^{t} \mathrm{tr}(A(\tau)) \, d\tau \right) $$

显然，$W(t)$ 表达式中 $e$ 指数部分恒大于零，只要 $W(t_0)$ 非零，即基础矩阵 $X(t)$ 在 $t=t_0$ 时刻线性无关，则在任意时刻均线性无关。因此，基础矩阵通常可以通过设置初始条件 $X(t_0) = I$ 来确定。

给定基础矩阵 $X(t)$ 和常数非奇异矩阵 $B$，取 $Y(t) = X(t)B$，显然有：

$$ \dot{Y}(t) = \frac{\mathrm{d}}{\mathrm{d}t} \left( X(t) B \right) = \dot{X}(t) B = A(t) X(t) B = A(t) Y(t) $$

因此 $Y(t)$ 也是一个基本矩阵。类似的方法可以证明 $X(t+T)$ 也是一个基本矩阵。

基础矩阵的一个重要特性是 $X(t+T) = X(t)B$，即基础矩阵在经理一个参数变化周期后，与原基础矩阵仅相差一个常数矩阵 $B$。

为了证明 $B$ 矩阵与时间无关，记 $Y(t) = X(t+T)$，不失一般性可以将基础矩阵一个周期内的变化表示为 $B(t) = X^{-1}(t)X(t+T) = X^{-1}(t)Y(t)$，于是根据定义有 $Y(t) = X(t)B(t)$，其初始为 $Y_0(t_0) = X(t_0)B(t_0)$；另一方面，前面证明基础矩阵右乘常数矩阵仍为基础矩阵，取 $B_0 = B(t_0)$，因此 $Y_0(t) = X(t)B_0$ 是基础矩阵，其初始也为 $Y_0(t_0) = X(t_0)B(t_0)$。相同的方程、相同的初值，对因的基础矩阵一定是相同的，因此有 $Y(t) = Y_0(t)$，进而得到 $B(t) = B_0$，即矩阵 $B$ 与时间无关。

为了得到矩阵 $B$，通常取 $t_0 = 0$ 和 $X(0) = I$，对原方程进行积分（可能需要数值方法），即可得到 $B = X(T)$。

Floquet 指数 $\mu_i \; (i=1,2,\dots,n)$ 与矩阵 $B$ 的特征值 $\rho_i \; (i=1,2,\dots,n)$ 之间的关系记为 $\rho_i = \mathrm{e}^{\mu_iT}$。可以证明原线性周期方程的解 $\bm{x}(t)$ 满足：

  1. $\bm{x}(t+T) = \rho \bm{x}(t)$
  2. $\bm{x}(t) = \bm{p}(t) \mathrm{e}^{\mu t}$，其中 $\bm{p}(t) = \bm{p}(t+T)$ 为周期函数

第一个性质的证明比较直接，记 $\bm{b}$ 和 $\rho$ 为矩阵 $B$ 的一个特征向量和其对应的特征值，取 $\bm{x}(t) = X(t) \bm{b}$，则有：

$$ \bm{x}(t+T) = X(t+T) \bm{b} = X(t) B \bm{b} = \rho X(t) \bm{b} = \rho \bm{x}(t) $$

对于第二个性质，取 $\bm{p}(t) = \bm{x}(t) \mathrm{e}^{-\mu t}$，则有：

$$ \bm{p}(t+T) = \bm{x}(t+T) \mathrm{e}^{-\mu (t+T)} = \rho \mathrm{e}^{-\mu T} \bm{x}(t) \mathrm{e}^{-\mu t} = \bm{x}(t) \mathrm{e}^{-\mu t} = \bm{p}(t) $$

由此可见，矩阵 $B$ 的特征值决定了周期方程解的包络：

  • 当所有特征值的模长均小于 1 时，通解将收敛到零，对应到控制系统就是满足内部稳定性；
  • 当存在特征值的模长大于 1 时，存在指数发散的通解，系统不稳定；
  • 当所有特征值的模长均小于等于 1 且存在模长等于 1 的特征值时，存在周期震荡的解，系统临界稳定。

考虑一个二阶弹簧阻尼系统，取状态变量 $\bm{x} = [x, v]$ 为位置和速度，则系统的状态空间方程为：

$$ \dot{\bm{x}}(t) = \begin{bmatrix} 0 & 1 \\ -\omega_n^2(t) & -2 \xi \omega_n(t) \end{bmatrix} \bm{x}(t) $$

假设系统的固有频率是随时间周期变化的，即：$\omega_n = \omega_c + \omega_a \sin\omega_d t$，则该系统为本文所讨论的线性时变系统。

假设该系统的标称固有频率为 3 Hz，阻尼比 $\xi=0.01$ 为定制，固有周期的波动范围为 0.1 Hz，波动频率分别为 5.9 Hz 和 6.0 Hz，在初位移条件下系统的位置响应如下图所示：

变频振荡器响应示意

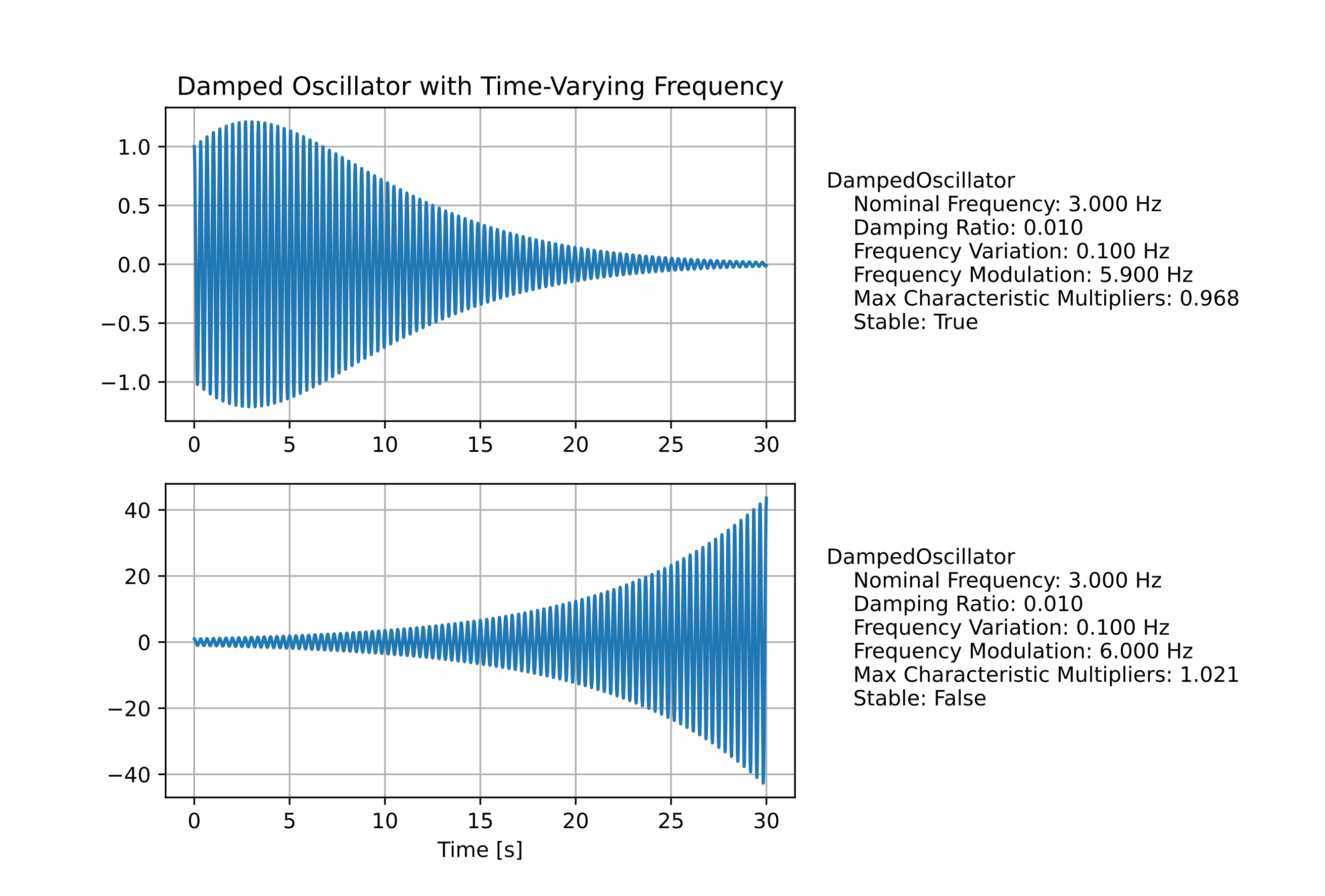
当参数波动频率为 5.9 Hz 时，系统对应 $B$ 矩阵绝对值最大的特征值为 0.968，系统稳定，因此位移响应将震荡收敛；而当参数波动频率为 6.0 Hz 时，系统对应 $B$ 矩阵绝对值最大的特征值为 1.021，系统不稳定，因此位移响应的包络将呈指数发散。

import numpy as np
import numpy.typing as npt
import matplotlib.pyplot as plt
import scipy

class DampedOscillator:
    def __init__(self, fc: float, fa: float, fd: float, xi: float = 0.01):
        self.fc = fc
        self.fa = fa
        self.fd = fd
        self.xi = xi

        B = self.get_floquet_matrix()
        self.eigvals = np.linalg.eigvals(B)
        self.max_eig = np.max(np.abs(self.eigvals))

    @property
    def info(self) -> str:
        info = 'DampedOscillator\n'
        info += f'    Nominal Frequency: {self.fc:.3f} Hz\n'
        info += f'    Damping Ratio: {self.xi:.3f}\n'
        info += f'    Frequency Variation: {self.fa:.3f} Hz\n'
        info += f'    Frequency Modulation: {self.fd:.3f} Hz\n'
        info += f'    Max Characteristic Multipliers: {self.max_eig:.3f}\n'
        info += f'    Stable: {self.max_eig < 1.0}\n'
        return info

    def __repr__(self) -> str:
        return self.info

    def simulate(self, t, x0: npt.NDArray[np.float64]) -> npt.NDArray[np.float64]:
        sol = scipy.integrate.solve_ivp(self.A, (t[0], t[-1]), x0, method='RK45', t_eval=t)
        return sol.y

    def A(self, t: float, x: npt.NDArray[np.float64]) -> npt.NDArray[np.float64]:
        mat = np.zeros((2, 2))
        mat[0, 1] = 1.0

        omega = 2.0 * np.pi * (self.fc + self.fa * np.sin(2.0 * np.pi * self.fd * t))
        mat[1, 0] = -omega**2
        mat[1, 1] = -2.0 * self.xi * omega
        return mat @ x

    def get_floquet_matrix(self) -> npt.NDArray[np.float64]:
        B = np.zeros((2, 2))
        for i in range(2):
            e = np.zeros(2)
            e[i] = 1.0
            sol = scipy.integrate.solve_ivp(self.A, (0.0, 1.0 / self.fd), e, method='RK45', t_eval=[1.0 / self.fd])
            B[:, i] = sol.y[:, -1]
        return B

if __name__ == "__main__":
    sys1 = DampedOscillator(3.0, 0.1, 5.9)
    sys2 = DampedOscillator(3.0, 0.1, 6.0)

    t = np.arange(0.0, 30.0, 0.001)
    y1 = sys1.simulate(t, np.array([1.0, 0.0]))
    y2 = sys2.simulate(t, np.array([1.0, 0.0]))

    fig = plt.figure()
    ax1 = fig.add_subplot(2, 1, 1)
    ax1.plot(t, y1[0, :], label='sys1')
    ax1.annotate(sys1.info, xy=(1.05, 0.5), xycoords='axes fraction', fontsize=10, ha='left', va='center')
    ax1.grid()

    ax2 = fig.add_subplot(2, 1, 2)
    ax2.plot(t, y2[0, :], label='sys2')
    ax2.annotate(sys2.info, xy=(1.05, 0.5), xycoords='axes fraction', fontsize=10, ha='left', va='center')
    ax2.grid()

    ax1.sharex(ax2)
    ax1.set_title('Damped Oscillator with Time-Varying Frequency')
    ax2.set_xlabel('Time [s]')

    plt.subplots_adjust(right=0.6)
    plt.show()
  1. Basic Floquet Theory. Michael Jeffrey Ward.
更新于 2026-02-04
阅读原始文档
 Floquet 理论, 周期系统, 稳定性分析
 | 主页